Smart Antennas and Beam-forming, Understanding with GNU : Part 3
Recap from part-2 of this article
Smart antenna systems or sometimes known as adaptive antenna array systems are composed of two major blocks; An adaptive antenna array block and a Signal processing block. Signal processing block is responsible for finding and adapting array beamforming weights and antenna array block uses those weights to give final system output. This output is nothing but a narrow beam directed towards a specific user and nulls are directed towards interfering users.
Performance of Antenna array block depends on following:
- Geometry of antenna array. Arbitrary array geometry or linear array geometry.
- Number of antenna array elements
- Spacing among antenna array elements. Uniformly spaced or arbitrarily spaced.
- Phase difference between elements.
- Performance of signal processing block depends on following:
- Type of algorithm used for estimating weights. For example, direction of arrival estimates or any other LMS, RMS based method.
- Further, Direction of arrival estimates also depends on what kind of algorithm is chosen. For example Root-MUSIC, ESPRIT, MVDR (minimum variance distortion less response) etc.
Smart antenna system’s performance depends on the performance of both the constituent blocks.
- The task of finding array beamforming weights is crux of the system and We limited our discussion to Root-MUSIC DoA estimation algorithm. We described mathematics behind this. In particular, we discussed correlation matrix which is a special case of the covariance matrix and eigen analysis of these matrices.
- We saw that correlation matrix consists of two orthogonal subspaces, noise subspace, and signal plus noise subspace. Eigen value decomposition, here on EVD, is a way to decompose correlation matrix into these two subspaces. We also saw an example of how EVD can be used for decomposing.
- One other important parameter that was not explicitly mentioned in previous parts of this article but It was buried under Octave script. This Parameter is called Antenna Array factor.
This can be defined as follows:

This can be further simplified to:

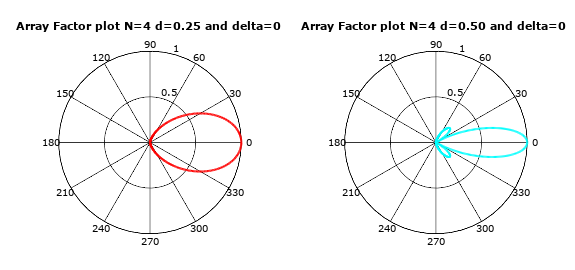
Let’s draw array factor plot for a simple uniform linear array with multiple distances using below octave script.

As can be seen from below output plots, the distance between antenna array elements is one major parameter for designing a beamforming array system. As this distance defines beam width.

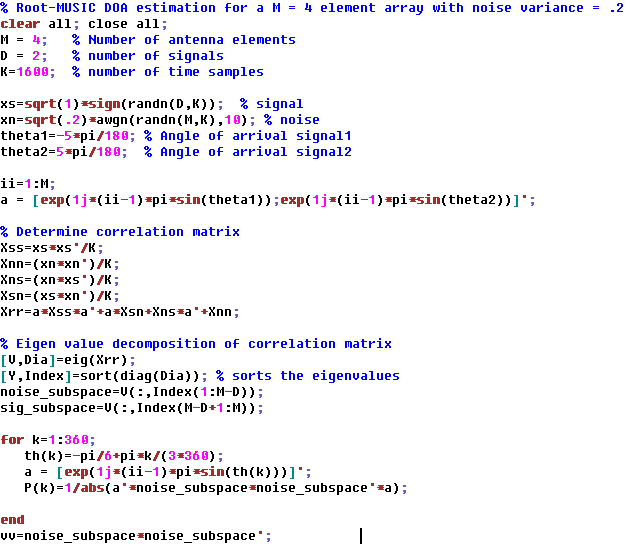
Now let’s focus on the Root-MUSIC algorithm of DOA estimation. The algorithm can be defined as following steps:
- Determine correlation matrix of the arriving signal, noise
- Determine Eigen vector and Eigen values of the correlation matrix. This splits correlation matrix into two subspaces, noise and signal + noise subspace. Remember that noise subspace corresponds to the maximum eigen value.
- Determine roots of the pseudo-spectrum polynomial.
- Determine the roots closest to the unit circle.
- Calculate the DOA by comparing to


Output of the above script is given below:

As can be seen from above that by using Root-MUSIC DOA estimation we were able to recover direction of arrival or angle of arrival of both the signals. (-5 and 5)
The problem of practicality
Although EVD of correlation matrix will give the best performance but , we have to take into account computational complexity for implementing EVD. It can be argued that EVD is not efficient to implement on real time systems even by using most advanced DSPs. Therefore, for practical reasons we need to find another way to achieve this decomposition. In fact, it turns out that Singular value decomposition or SVD are related to EVD, and SVD is more efficient to implement on modern DSPs.
It is worth mentioning here that it is not just about computational complexity. The dynamic range of EVD is twice that of a SVD. More the dynamic range of an algorithm more it is a problem while implementing it on a fixed-point DSPs.
Maybe next time, we will see a comparison between SVD and EVD.
Article Submitted By Mr. Dheeraj Sharma

Dheeraj Sharma is working as LTE-A/5G Physical Layer ( DSP) Engineer. He has expertise in DSP/Physical layer firmware development, Integration and optimization in multiple Radio Access Technologies (GSM/GPRS/EDGE, GMR-1 3G, LTE,xDSL)